I was recently thinking about the endgame tablebases. There's a really nice website which allows you to input an endgame with 7 or fewer pieces and see the theoretical state of the game.
I wasn't sure where to look, but I was wondering what kinds of statistics have been collected from this data. For example, what percentage of games are draws (with/without the 50 move rule). The best I could find was this blog post which only discusses the 5 piece table base, and also didn't include more general statistics.
My thought is that this could give some insight into the theoretical state of chess overall. If we imagine that theoretically perfect play leads to one of these endgames randomly, then we can asses the likelihood that chess is a theoretical draw.
I would download the tablebase and look for myself, but I do not have the resources to store and parse over 8 terabytes of data.
They have the 7 piece tablebase here too.
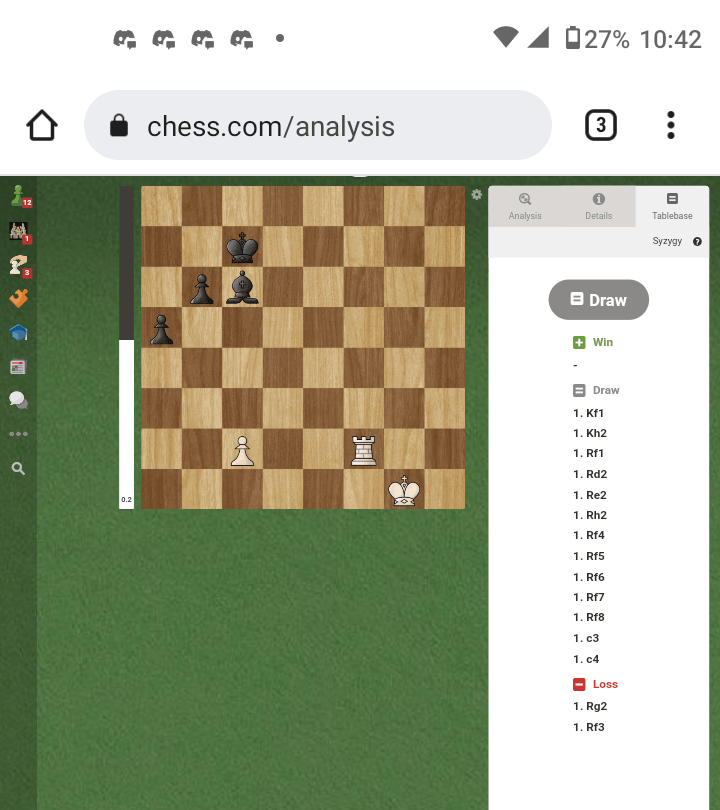
I was recently thinking about the endgame tablebases. There's a really nice website which allows you to input an endgame with 7 or fewer pieces and see the theoretical state of the game.
I wasn't sure where to look, but I was wondering what kinds of statistics have been collected from this data. For example, what percentage of games are draws (with/without the 50 move rule). The best I could find was this blog post which only discusses the 5 piece table base, and also didn't include more general statistics.
My thought is that this could give some insight into the theoretical state of chess overall. If we imagine that theoretically perfect play leads to one of these endgames randomly, then we can asses the likelihood that chess is a theoretical draw.
I would download the tablebase and look for myself, but I do not have the resources to store and parse over 8 terabytes of data.