Minimal moves for checkmate King + Queen vs King

Hello, 

although i looked for this topic anywhere on internet, I didn't find anywhere a reliable method explaining how to checkmate a King with a King and a Queen with MINIMAL NUMBER OF MOVES (only those pieces are on the board). I know this mate is an elementary case for beginners, but most of times whenever i'm trying to do a move, the engine says there is quicker way to checkmate with less  moves (1 to 3 moves less).

So my question is : depending on the initial position of King + Queen and opponent's King, what is the method to checkmate in minimal moves ? Is there a way to think ? a vision mathematical method ? 

Thanks for answer, regards, 

Jyloup

I know it's 9 moves from the worst position in general case, but my question is from the actual position ? Depending on the initial position it could be between 1 and 9 move but how to calculate it easily ? how to make the optimal moves ?

Interesting question. I'll work on it. If I find some general mathematical method, I'll post it here.

Ok great if you find a method! 

Have you tried the drill? It tells you if your move was "best possible" at each stage. Try to generate a hypothesis and test it with experiments:

https://www.chess.com/drills/practice/queen-mate

Here's something that partially worked, got me "best possible move", until BK hit the edge of the board, then I went a bit wrong...

After opposing King (BK) moves:

1) Move your Queen (WQ) to contain BK in the smallest possible square of territory.

2) After BK, moves repeat 1), unless you can't reduce the territory (cause WQ would be taken...) In that case move WK closer to the WQ by the shortest path. That gets WK to a square where it can help WQ reduce the territory available to BK.

I'll leave you to see if you can come up with the rest of the solution, jyloup.

P.S. click on the light bulb icon and the software show you the best move!

How about start by solving this for a 4x4 board, then try to expand from there. I don't like the idea of just getting heuristic rules that seem to work. I'm a mathematician, this problem needs to be solved.

All right, in order to study this question, I adopted the following strategy. Let's place first the black king. By symmetry, we can suppose that it's located in the upper right square with vertices e5-e8-h8-h5. Now let's place the white queen somewhere and study how solutions vary depending on the position of the white king. The first example:

Notations: Q = white queen, K = white king, k = black king, dist(K,k) is the distance between kings. The distance on the chessboard is measured by the number of king's moves.

Generic solution: There is a quickest mate in dist(K,k) moves starting with Qa7 and/or Qg2.

Exceptional cases:

1. The mate in 1 move Qa8# or Qh2# while dist(K,k)=2 when K is placed on f7-f8 or g6-h6.
2. The mate in 2 moves starting with Kf7 while dist(K,k)=3 when K is placed on e8-e7-e6-f6.

In the same manner we can treat all cases when the black king is on h8 (or, by symmetry, in any other corner).

Generic solution: There is a quickest mate in dist(K,k) moves. As the first move, U should put Q on the 7th row or g-file, then approach the white king.

So, we treated 1/8 of all cases. Indeed, we can take into account diagonal symmetries. So, it's sufficient to consider only the following 8 positions of the black king: e5, f5-f6, g5-g7, h5-h8.

So now i need to compute the minimal moves for each elementary cases of 8 positions of black king and find a visual way to apply it in practical cases. Let me some time to publish it here.

I like my method. My background's in physics, there is no time to seek out a perfect mathematical proof, better accept the simple heuristic, and get on with more important stuff, like winning games.  Only joking, of course, whatever floats your boat.

All right. The cases when the black king is on the rim (h5-h7) are somewhat similar.

U can use Shredder's Endgame Tool based on Nalimov's tablebases:

http://www.shredderchess.com/online-chess/online-databases/endgame-database.html

It's quite practical.

Yeah, your heuristic method is quite good but some people like exact mathematical solutions.

I worked on this a bit last night actually. I was going to start a Microsoft word document (more like a book) called "an exhaustive guide to checkmating with a king and queen."

There are 10 unique black king positions, so it would have 10 chapters.

Unfortunately it does seem there are just way too many possibilities. However, I have found another good heuristic. The only possible way for checkmate to occur is if the white king is inside the square centered around c3 - f3 - f6 - c6. He cannot give checkmate adjacent to the edge or two sqares from the edge. Therefore, I think exhaustive solutions should start with the idea of the white king being inside this square. Then we can work out more solutions by transposing to those known situations where mate is possible.

So each chapter would be an exhaustive guide to mating with the black king on a specific square. So the first would be the corner. Luckily, some positions are easy to solve.

With the black king in the corner and the white king in the corner (of his smaller square) every possible queen position is a mate in one except for the one shown, which is mate in two. This seems like a common positions to transpose to.

With the white king here (I forgot about this exception to the center square rule) every possible queen position is mate in two. The queen simply goes to the e file, then gives mate.

It might be interesting to keep going for an entire chapter, but I'm having trouble figuring out exactly how to do it, and it's not helping solve the problem.

I'm pretty sure there might be what we call "equivalence classes" in term of number of moves to mate.

I must find the main features of positions mate in 9, mate in 8, etc.. until mate in 1.

All positions in the same equivalence class have the same number of moves for mate (white to play at start). Similarly, the different moves leading to the same minimal mate are in the same equivalence class.

For example, in the example below, the queen and/or king moves leading to this optimal mate in 8 are limited (see notations), so we consider all those moves are in the same equivalence class. All other moves leading to mate in 9 are in another equivalent class, and so on. I must now find a key feature about the position to understand why it's 8 here, why it's those moves.

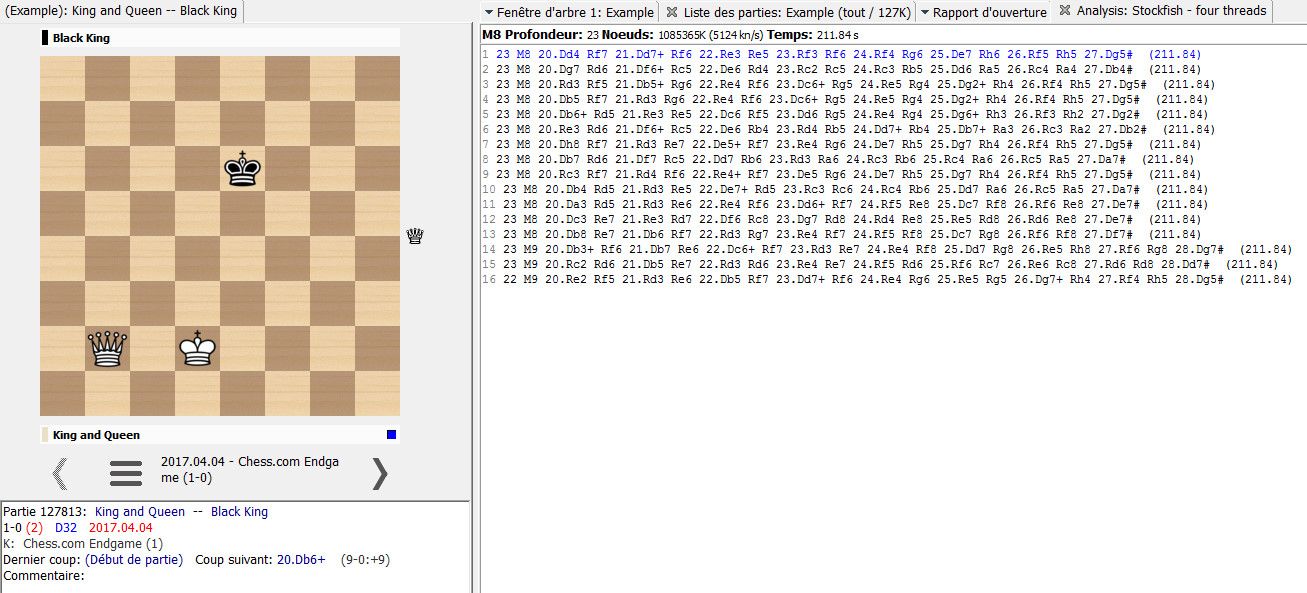
In this example, only 3 moves lead to mate in 7 :

according to the engine :

Probably the features to observe could be the initial distance between 2 kings, if Black king is between the white king and queen, on opposite side, the territory, etc...

Let me some time to discover an easy way to know the equivalence classes, after some empirical observations.

Are you still interested in the answer? I can help here.

The tablebases (like lomonosov) have been constructed to precisely answer that question. Why is that necessary? The answer is that any diagram presented may already have been underway for a while with just aimless moves. So a diagram with K+Q vs K may be underway to the 50-move line and is now at the 84 half-move point (without capture or pawn move). Then it's really urgent to complete the mate within the next 8 full moves or a 50-move draw claim will be made.

The algorithm is simple. Pick the next move from the properly indexed tablebase together with the related distances to mate or the next capture/pawn-move. It is the perfect algorithm and it yields the perfect answer so there is no reason to complain.

You probably wonder how the tablebase was generated but that's not really relevant for answering the question. Also, it is pretty simple. Just recurse backward from all endgame checkmate positions and you'll subsequently get all winning positions 1 move from mate, 2 moves from mate .... 564 moves from mate. Even a kid could write that program! Provided he owns a cloud computer with sufficient power and storage to work through trillions of positions.

So, are there heuristic methods to reduce the tablebase size or its generation speed? Well, there probably are but who cares? I suppose just those who ultimately want to solve chess in this fashion and not just the positions with up to 7 units. That's where science currently stands.

So many things wrong here. But not limited to... 9 is not max. 10 is... Example. Ka1 Qb2/Ke6 or Kf5 for starters...