Relative ELO vs. expected win/loss ratio?

Anyone know a formula to relate ELO to expected win/loss ratio? For example:

"A 1300 ELO player facing a 1000 ELO player, is expected to win X out of Y times"

Is there a general formula? If you also include white / black advantage that's fine, I am just interested in how ELO translates to win odds.

Thanks. Do you think this scales linearly? Like a 500 vs 400 is the same odds as a 2500 vs 2400?

Idk a formula but I found this thing online: https://wismuth.com/elo/calculator.html It's not presented as The Truth, but there's a mathematical justification below it so you can see if you're convinced by the reasoning.

A formula exists, but it involves advanced mathematics: the error function
https://en.wikipedia.org/wiki/Error_function

A table is easier.

Also, it is Elo, not ELO. It is not an acronym, it is the name of the guy who invented it.

don't care too much about your opponent's elo, this makes you afraid of the opponent.

Also, I don't think there is such a formula

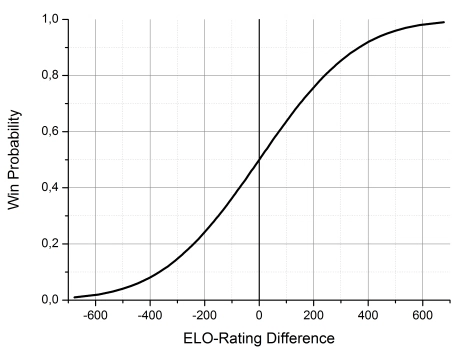
expected_score = 1 / (1 + 10(RatB - RatA)/400).

from https://www.omnicalculator.com/sports/elo

(RatB is opponent rating, RatA is your rating, expected score is your chance of victory)

Here you go:

https://www.318chess.com/elo.html

Read the text after the table for further explanations, but in essence if it says 75% it doesn't mean that you will win 3 games, but it means that you will have a score 3 out of 4 after 4 games on average, which could be 3 wins or 2 wins and 2 draws for instance.

Correct. But then chess.com adapted the formula taking into account the estimated accuracy of the rating, new players with few games played get their ELO adjusted more. But after some 30 games or so that factor is so low that you get the same result as the standard ELO formula.

For fun (yeah I'm kind of a nerd sometimes) I took all my games played at chess.com into excel to see what coefficients gets the most accurate prediction based on my results and the relative difference in rating towards my opponent. And I get the best predicted outcome (lowest standard deviation) if I change the 400 factor to 140. Which means that I have lower chances to win against a stronger opponent than the original formula predicts (and vice versa).

Perhaps it would be a bit more accurate if you would exclude the first 10-20 games you've played (until your rating gets more stable) and exclude any opponent with less than 10-20 games.

But in any case, the more games included the more accurate it should be.

Here is a graph showing average result (y-axis) vs difference in rating (x-axis). Blue = based on my games played, orange = original ELO formula.

I did not include my first games, I think it was around 200 games in total. But now I've played more than 1000 games so maybe I'll do another calculation to see if I get the same result. And I can also see if there is a difference now when me and my oponents area little higher rated. I'm still not a very strong player though, my current rating is 1100 but when I did these calculation I think it was more like 700-900.

#15
The orange line is wrong: the relation is not linear but involves the error function
#9
Yes, there is a formula, but it involves the error function

It looks linear because it only shows low differences in ELO. I didn't have enough games with higher difference because chess.com mostly pairs me with players +/- 100 my own rating.

From internet

100 difference is 100 difference, it is the same. The difference between players is what matters. Now, of course all of this is for people with established ratings, so they need to play some games in order for their rating to stabilize.

So if a player played let's say 20 rated games (not sure how many exactly, it can depend on how off is your initial assessment about your playing strength) and his rating is somewhat steady around 400, and the other player with same conditions have a rating of 500, the second player will approximately have 2 out of 3 score after 3 games played on average.