
Quantas partidas são possíveis no xadrez?
Quantas partidas possíveis existem no jogo de xadrez?
Há um fato popular que diz que o número de partidas possíveis no xadrez é maior que o número de átomos no universo.
A estimativa deste número de partidas do jogo de xadrez é conhecido como Número de Shannon, dado pelo cálculo do matemático Claude Shannon, em 1950.
No seu livro "How to program a computer to play chess" ele descreveu uma estimativa de quantos jogos seriam possíveis: aproximadamente 10 elevado a 120ª potência, ou seja, o número 1 seguido de 120 zeros à direita, sendo maior que a quantidade de átomos do universo observável (≈10 ⁸⁰ ).

O método de Claude Shannon era baseado nos dois seguintes pontos: a cada posição, o jogador terá mais ou menos 30 movimentos possíveis e o jogo de xadrez dura em média 40 lances (40 movimentos para as brancas e mais 40 para as negras) e a cada posição um jogador terá mais ou menos 30 lances legais, entretanto a fórmula seria de 30 elevado a 80ª potência, que resultaria no Número de Shannon:
30⁸⁰ ≈ 10¹²⁰

Esse número encolhido pode parecer menor do que realmente é, mas pensando que até o lance 2 de um jogo podem existir 197.742 continuações diferentes, já existe uma boa ideia da proporção do imenso número.

Essa áspera estimativa foi feita com o intuito de mostrar de se você tivesse um computador que jogasse xadrez e ele estivesse tentando calcular o futuro exato da partida, nunca faria um lance, pois se estivesse pensando em todos os lances legais e o final de cada variante, levaria trilhões de anos, mesmo que a máquina calculasse 1.000 linhas por segundo.

Em resumo, o que Claude quis dizer é que em 40 lances existirão aproximadamente 10¹²⁰ partidas , mas apenas em 40 lances, desconsiderando outros jogos mais longos.
Portanto, um dos matemáticos mais famosos do século XX, Godfrey Hardy, a pedido do matemático indiano Srinivâsa Râmânujan, estimou o número de todos os jogos possíveis como 10 elevado ao resultado de 10 elevado a 50ª potência, o mesmo que o número 1 seguido de 500 zeros à direita.
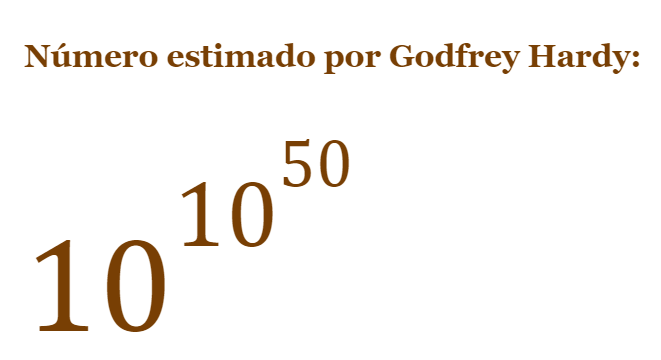
Esse número é imensamente abundante em comparação ao Número de Shannon, porque abre muitos outros caminhos para partidas mais longas que seriam quase impossíveis de se obter em um jogo "comum".

Considera-se então cada partida (uma por uma, mesmo que existam jogadas completamente absurdas) como um minúsculo galho desta imensa árvore de possibilidades.

Porém, uma partida de xadrez não dura para sempre, mas sim até aproximadamente 5900 lances, que é a média do limite de lances que se pode jogar sem que haja um empate pela regra dos 50 lances ou outro resultado.
Enquanto que o número de partidas do jogo de xadrez é inimaginável com sua grandeza, a quantia de partidas já jogadas na vida real é uma pequeníssima fração deste número. E é por isso que é matematicamente impossível resolver o xadrez.
⁸⁰ ⁸⁰
